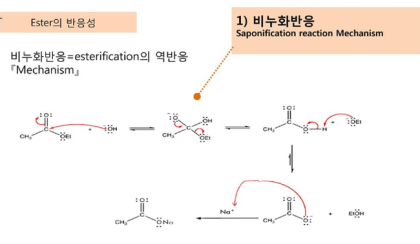
Add 50mL of a 0.02M weak acid (pKa=6.72) solution to 0.1MNaOH solution. What is the pH at the equivalent point?
① Neutralization reaction by NaOH A Hydrolysis reaction of A-anions HA+OH→A-+H2O(acid base neutralization reaction)$NaOH solution volume required =\frac{0.02M\\times50mL}{0.10M}=10mL$NaOH solution volume required = 0.02M×50mL0.10M=10mL
$\left[\combi{]A}^-\right] =\frac{0.02M\x50mL}{\left(50+10\right)mL}\ = 0.01667M\ $[A-] = = 0.02M×50mL(50+10)mL = = 0.01667M
[A-][HA]-[OH-]I0.0166700E0.01667-××$\combi{pK}_b=14-\combi{pK}_a=14-6。72=7.28ドルpKb=14-pKa=14-6。72=7.28$\combi{K}_b\ =\frac^combi{x}^2}{0.01667-x}\ =\\\combi{10}^{-7}.28}\ =\5.25\times\combi{10}^{-8}$Kb=x20.01667-x = 10-7.28 = 5.25×10−8$\combi \x\ =\left[\combi{OH}^-\right] =\sqrt{0.01667\times 5.25\times \combi{10}^{-8}}=2.96\times \combi{10}^{-5}\M$ph x = [OH-] =√0.01667×5.25×10-8=2.96×10-5 M$pH\\log\left(2.96\combi{10-47\right=14_右)\times =14_472:247}$\combi \x\ =\left[\combi{OH}^-\right] =\sqrt{0.01667\times 5.25\times \combi{10}^{-8}}=2.96\times \combi{10}^{-5}\M$ph x = [OH-] =√0.01667×5.25×10-8=2.96×10-5 M$pH\\log\left(2.96\combi{10-47\right=14_右)\times =14_472:247}


